For the above question to even start to make sense, let’s make one main assumption: let’s say that plain text has dimension one, whereas pictures of faces, landscapes, and other objects, have dimension two. Here is the case for assigning dimension one to plain text. In English, and other European languages, verbal information is encoded in written form by means of the alphabet, writing down one character at a time, in a linear sequence. We create words by placing letter after letter in a given sequence. We create phrases, and sentences by placing word after word in a given sequence. In practice, text lines are broken according to the width of each page, and pages are filled with many lines of text. However, in the abstract model for this way of encoding information, we can consider each text document as a single, long, uninterrupted line of text. To read text, we only need the basic linear connection from each letter to the next one, and from each word to the next one. Any text document can be considered as a sequence of characters, however long it may be.
On the other hand, when we look at images in the real world, like homes, people, faces, mountains, trees, animals, and so on, we process this visual information in a very different way. We see color, shades of color, light, texture, and a multitude of details that can only make sense when we consider them embedded in the full three-dimensional space around us. However, our retina is pretty much a flat surface, and our brains have to imagine the three-dimensional world based on the two-dimensional information our flat retina collects from the incoming light. So, the raw material our brain uses to process visual information is nearly two-dimensional in nature. When looking at an image, if we consider a little part of it, there is no such thing as “the next pixel,” because that could be located above, or below, or to the right, or to the left, or in any diagonal direction. Often we can find linear patterns inside some images but the whole image is fully two-dimensional.
So, where does this basic assumption about dimensions leave the written representation of mathematical expressions?
In a recent math tutoring session, I was helping a student prepare for the SAT, and we came across a problem that involved the expression a(1/2). However, we got confused for a couple minutes because there were no parenthesis around the fractional exponent, the exponent was in a font size as big as that of the variable, and the fraction bar was too close to the variable. It looked something like this:
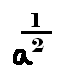
So, at first we thought the book meant 1/(a2). We momentarily (and incorrectly) interpreted the expression as if it had looked like this instead:
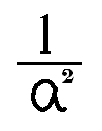
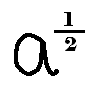
We were trying to solve the problem doing the calculations with that interpretation, and we were getting nowhere near the answer, until we realized the book meant a(1/2), not 1/(a2).
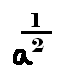
So, at first we thought the book meant 1/(a2). We momentarily (and incorrectly) interpreted the expression as if it had looked like this instead:
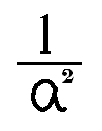
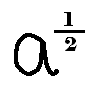
We were trying to solve the problem doing the calculations with that interpretation, and we were getting nowhere near the answer, until we realized the book meant a(1/2), not 1/(a2).
The expression should have looked more like this:
This simple example shows that, when reading mathematical expressions, we process the information in a way that seems like a hybrid of how we read text, and how we look at two-dimensional images. In reading math expressions, it is very important to take into account visual clues like the size of each symbol, and the relative position they hold to each other, their spatial arrangement in the page, and how close or far away they are from each other. This is essential because mathematical notation implicitly uses our instinctive understanding of two-dimensional images to convey the fine details of each expression’s precise, hierarchical structure. This also has to do with the familiar PEMDAS rules of evaluation, and is key to getting the problems right. Correctly applying the PEMDAS rules is relatively easy when a particular expression is all contained in a line of text. However, when we start dealing with sub-indexes, summation notation, roots, integrals, derivatives, rational functions, powers of powers, upper and lower limits, fractions of fractions (and especially with combos of all of the above); deciphering an expression's structure requires a visually detailed inspection of the two-dimensional arrangement of all the different symbols making up the expression.
As opposed to a line of text, the structure of a mathematical expression is not necessarily linear. Most often than not, the hierarchy branches out. Mathematical expressions include symbols for operations. Operations usually are functions of two arguments, or parameters. These are called "binary" operations, like addition, or multiplication. Often we work with "unary" operations, or functions of only one argument, like the square of a number, or its absolute value. Sometimes we work with operations that take more than two arguments. The basic fact is that functions have input arguments, and produce output values that can, in turn, be used as inputs by other functions. A mathematical expression has a hierarchical structure given by all the connections between input values, and the functions using them. The written representation of a math expression has to present all these connections unambiguously. The set of all these connections between symbols constitutes a hierarchy that we call a rooted tree. This term (bear with me) denotes an acyclic, connected, directed graph with a finite set of nodes, including one main node (the tree’s “root”). Upon this underlying structure, each node gets associated with a particular symbol representing either a constant, a variable, or an operation. Let’s look, for example, at the quadratic formula (the formula used to solve quadratic equations):
This simple example shows that, when reading mathematical expressions, we process the information in a way that seems like a hybrid of how we read text, and how we look at two-dimensional images. In reading math expressions, it is very important to take into account visual clues like the size of each symbol, and the relative position they hold to each other, their spatial arrangement in the page, and how close or far away they are from each other. This is essential because mathematical notation implicitly uses our instinctive understanding of two-dimensional images to convey the fine details of each expression’s precise, hierarchical structure. This also has to do with the familiar PEMDAS rules of evaluation, and is key to getting the problems right. Correctly applying the PEMDAS rules is relatively easy when a particular expression is all contained in a line of text. However, when we start dealing with sub-indexes, summation notation, roots, integrals, derivatives, rational functions, powers of powers, upper and lower limits, fractions of fractions (and especially with combos of all of the above); deciphering an expression's structure requires a visually detailed inspection of the two-dimensional arrangement of all the different symbols making up the expression.
As opposed to a line of text, the structure of a mathematical expression is not necessarily linear. Most often than not, the hierarchy branches out. Mathematical expressions include symbols for operations. Operations usually are functions of two arguments, or parameters. These are called "binary" operations, like addition, or multiplication. Often we work with "unary" operations, or functions of only one argument, like the square of a number, or its absolute value. Sometimes we work with operations that take more than two arguments. The basic fact is that functions have input arguments, and produce output values that can, in turn, be used as inputs by other functions. A mathematical expression has a hierarchical structure given by all the connections between input values, and the functions using them. The written representation of a math expression has to present all these connections unambiguously. The set of all these connections between symbols constitutes a hierarchy that we call a rooted tree. This term (bear with me) denotes an acyclic, connected, directed graph with a finite set of nodes, including one main node (the tree’s “root”). Upon this underlying structure, each node gets associated with a particular symbol representing either a constant, a variable, or an operation. Let’s look, for example, at the quadratic formula (the formula used to solve quadratic equations):
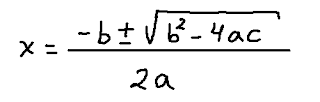
Below we show the rooted-tree that is the foundation for the hierarchical structure of the quadratic formula (not including the equal sign, just the right-hand side); along with the constants, variables, or operations that are associated to each node in the graph. Looking at the arrows, you can see each individual symbol is connected to the one directly “above it” in this hierarchical structure:
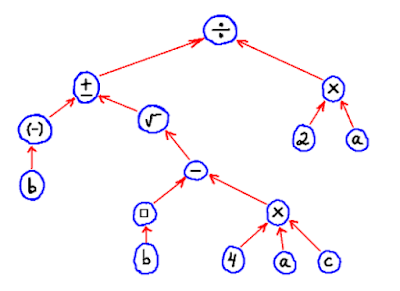
In the diagram above, I use the square shape to represent the application of the function "taking the square of b." Note we are still making an implicit assumption based on our visual processing of images. We are relying on the left-right distinction to implicitly give the correct ordering for the arguments of division, and subtraction, the two operations used here that are not commutative.
The rooted tree makes apparent the formula's underlying, hierarchical structure, it shows all its components, and their individual connections. We could philosophically argue that this structure is what the quadratic formula "really is," independently of the format we choose to represent it. My purpose here, in showing the rooted tree associated with the formula's structure, is to make the point that the linear simplicity of written text falls short when it comes to encoding complex mathematical expressions. True, with suitable conventions, and enough parenthesis, you can make almost any math expression fit into a line of text but that does not make its structural complexity go away one bit. For example, you can write the quadratic formula like this:
x = (-b [+/-] sqrt(b^2-4ac))/(2a)
It is all written in a line of text but the hierarchical, branching order of its operations is still the same. Many students (and, consequently their math instructors) deal all the time with the relative difficulty of correctly deciphering the hidden structure of mathematical formulas based on its written representation. This is a fundamental skill that heavily affects students' performance in math, and therefore, their grades, and their future career choices.
Not long ago I wrote a related post in this blog, titled "Math is not English."
People who are not "math-oriented" may find this hard to believe but actually, the mathematical syntax, symbols, notation and conventions currently in use (at least up to Calculus and Linear Algebra) are pretty much the easiest, clearest, simplest, most convenient way mathematicians have found (laboriously through the centuries) for writing and reading mathematical formulas. Believe me, the guessing and reasoning behind the formulas is hard enough. No mathematician is interested in making the notation artificially complicated, quite the contrary.
This finally leads me to the reason why I wrote this post in the first place. I recently attended an online get together of fellow Twitter math enthusiasts. The discussion centered on the large gap between text editors, and math equation editors; particularly with the purpose of publishing, storing, and searching mathematical expressions on the Internet. Compared to the wide availability of high-quality word processors, text editors, and text-based search engines, there seems to be a perceived scarcity of free, online tools for authoring and delivering math expressions online, as well as for searching math documents by their mathematical formulas, not by keywords. These topics immediately made me think of the fundamental structural difference between text and math I mention above because, as a math tutor, I have to help my students deal with this chasm practically every day.
Mathematicians would absolutely love a software package capable of identifying, and extracting the hidden, hierarchical structure of a math formula from the handwriting they could do on an electronic tablet with an electronic pen. My contention is that one of the main reasons this type of software does not yet exist, is because of the large extent to which the conventions of current mathematical notation rely on our unconscious, instinctive, biologically hard-wired, visual processing of images to convey mathematical meaning. As crazy as it sounds, and no matter how many of my students I know would disagree with this statement, we have come a long way in making math very easy to read and write on a piece of paper. However, we have done so by tapping into our biological processing of images, and this has inevitably put us at a disadvantage when it comes to entering that information into a digital format.
Anyway, the question in the title of this post: "Is there a connection between Mathematical Writing and Fractal Geometry?" is motivated by the non-linearity (branching out) of hierarchical math expressions, on one hand, and our hybrid way of reading them, on the other; as something between dimension one (plain text), and dimension two (full images).